欠了好久了,有些东西就先跳过了,后面有时间再补吧,先把一些感觉之前没有学的很懂的东西再捋一遍。
语法制导翻译技术
在翻译文法的基础上,扩充了值的概念。
属性
综合属性

于是在表示属性计算的语法树上就可以通过这样向上传递的返回值得到表达式的结果,于是进一步的,规则可以改写为一下形式:
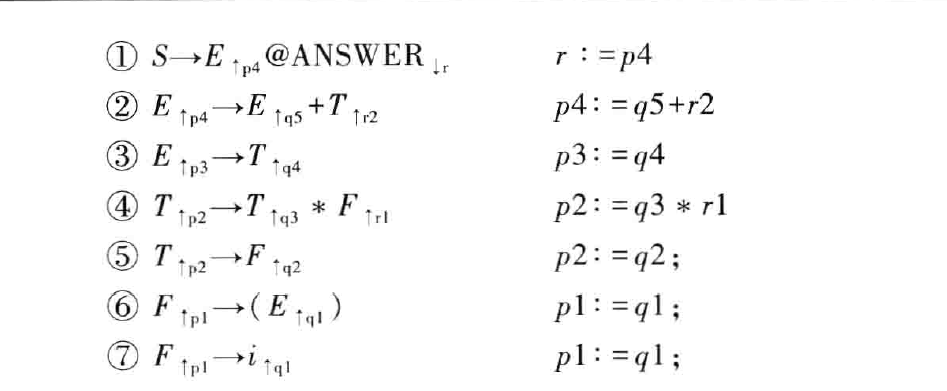
右边的式子可以被称为求值规则,其对应的语法树如下图
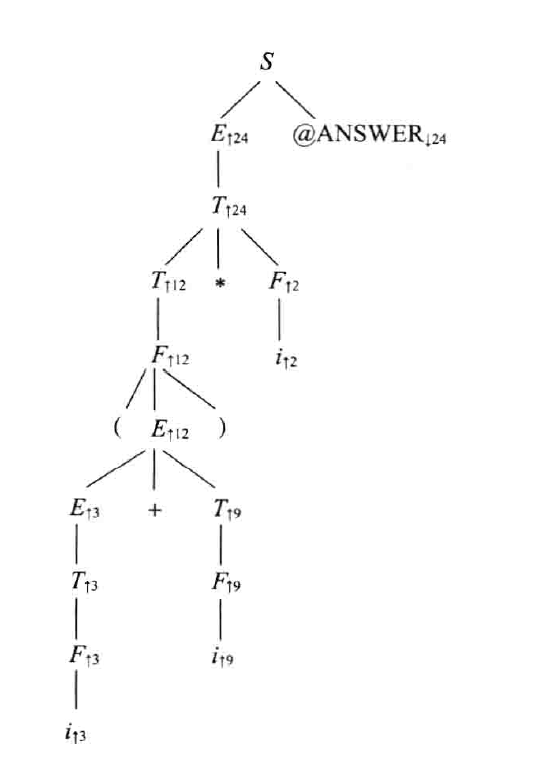
这样通过自底向上进行求值的属性也被称为综合属性。类似于递归时,一层层得到的返回值。
继承属性
其很多时候会作为动作符号所需的参数从而进入规则当中,而对于动作表中的参数,也就是向下传到的值,其必须在本条规则中有来源,一般是由在他左边的值传递得到。而这时的值又可以分为两种,一是从上一条规则传递下来继承得到,一是由底层的返回值得到。

如上面的第②条规则中,变量表的$t_2$就是从上一条的$t_1$传递下来的,因此为↓,而id的值可以词法分析程序返回值得到,因此可以为↑。
对比来看,综合属性式自底向上的属性传递,而继承属性式自顶向下、自左向右的属性
属性翻译文法
满足条件
- 文中的终结符、非终结符和动作符号都带有属性。
- 非终结符和动作符号属性可以分为继承属性和综合属性
- 开始符号的继承属性具有指定初值(可以从传参角度来看)
- 终结符号的综合属性具有指定初始(叶子函数的返回值)
- 继承属性求值原则:产生式右部符号的继承属性值,用该产生式其他符号的属性值进行计算。若是左部的非终结符,则继承前面产生式该符号已有的继承属性值/
- 综合属性求值原则:
- 尝试左部非终结符号的综合属性值,用该产生式左部或右部的某些属性值进行计算
- 动作符号的综合属性值,用该符号的其他属性值进行计算。同若为右部产生式,其为其作为下部产生式的左部时所得到的综合属性值
给定一属性翻译文法,由该文法可得到由属性输入符号和动作符号所组成的属性活动序列,这个属性活动序列的动作符号序列便可以被称为对属性输入符号序列的翻译。
算术表达式翻译举例
其输出格式为四元式,一个运算符,两个指向操作数的指针,一个指向运算结果的指针。 其翻译程序的设计可以分为两个部分,分别为设计翻译文法和构造属性和规则
设计翻译文法
一般是构造有关输出的动作符号。算数表达式的动作符号明显就为输出四元式,因此可以设计两个动作符号@ADD和@MULT。那么就是其放在规则$E \rightarrow E + T$的那个位置,显然如果要能把各个操作数的地址输出,那么自然其要放在进行操作之后.因此翻译文法可以得到$E \rightarrow E + T @ADD$
构造值和规则
通过构造之后,这个文法能够计算输出符号的值。
容易得到右部的给符号的值一般都是在下面的产生式传递上来的,因此其为综合属性。而左部得到的符号也是需要向更上一级传递,因此其也为综合属性。而终结符号所需的参数正式操作数的地址,为继承属性,且无需返回值,所以不需要综合属性
因此最后的规则可以得到如下形式:
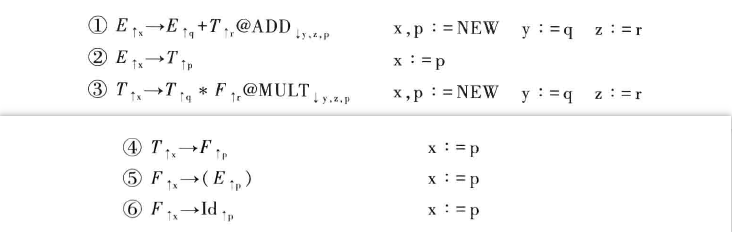
L属性翻译文法(L-ATG)
针对LL1文法,比起上述的规则,在继承属性和综合属性的取值规则又多了限制
- 继承属性
- 产生式左部的继承属性取前面产生式右部该符号的已有继承属性
- 产生式右部的继承属性由该产生式左部符号的继承属性或该符号左边的符号属性值得到
- 综合属性
- 产生式右部符号非终结符(终结符有指定的初值)的综合属性取下部产生式左部同名的综合属性
- 产生式左部的综合属性值用该产生式左部符号的继承属性或某个右部符号的属性得到
- 动作符号的综合属性用该动作符号的继承属性或者右部符号的属性得到
用下面图可以概括上述情况、
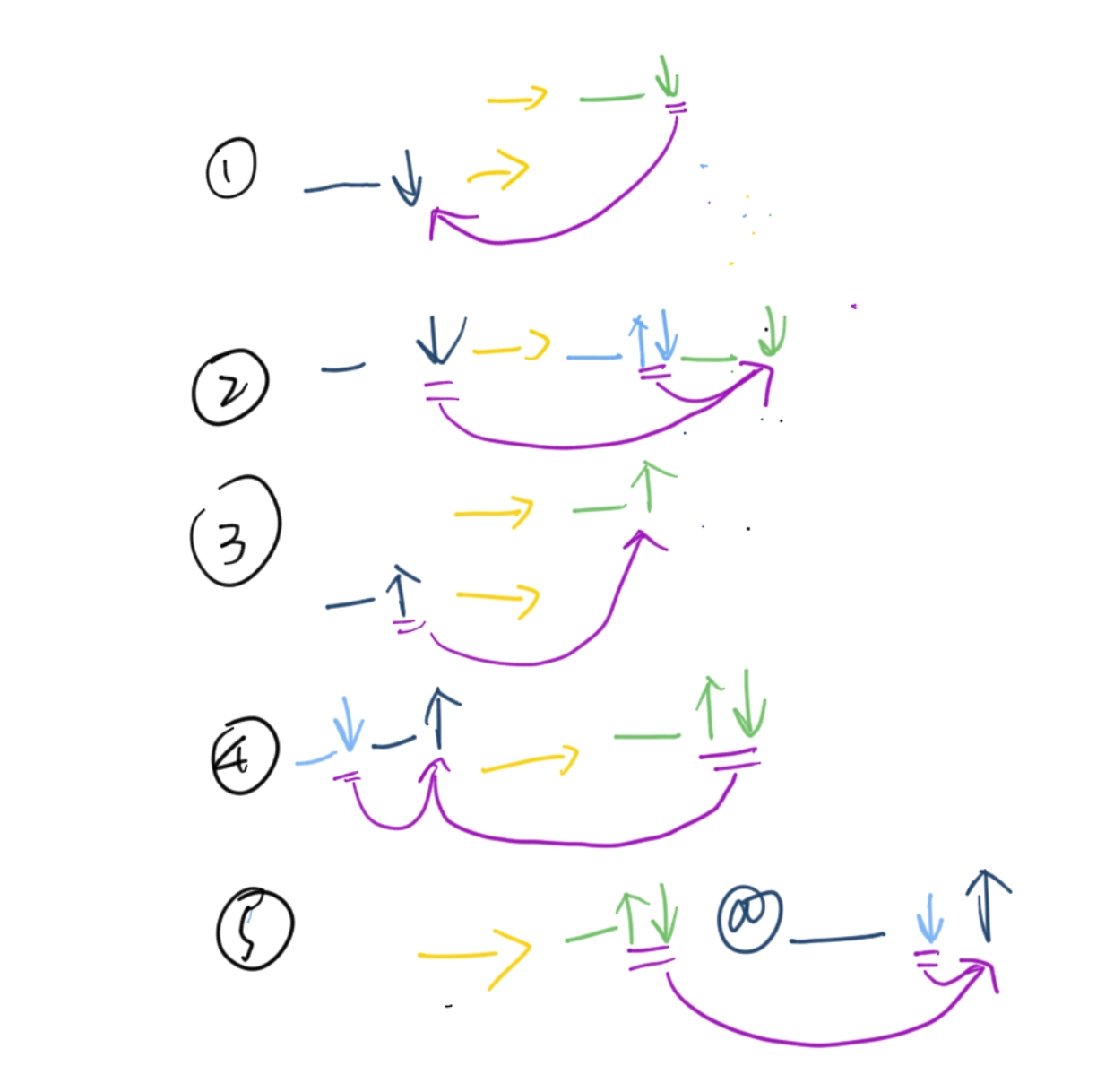
上述继承关系体现了自顶向下,自左而右 的特性,而综合属性也体现了自底向上,自右向左的特性。(上图可以把顺序重排一下更明显)
SL-ATG
定义
将属性规则写成赋值语句时可以这么表述, $x := f(y, z)$, 但可以用简单的赋值$x, y := z$这样来表示的属性规则,就可以称为ST-ATG. ST-ATG 要在L-ATG的基础上满足以下两条条件:
- 产生式的右部符号的继承属性是一个常量,等于左部符号的继承属性值,或等于出现在符号左边的符号一个综合属性值
- 产生式左部非终结符的综合属性是一个常量,等于左部符号的继承属性或时右部符号的综合属性值。
因此ST-ATG的属性求值规则其右部是属性或者常量。(不可能是表达式)。给定L-ATG可以通过增加动作符号的方式构造等价的SL-ATG
转变方法
本质上是让动作符号表示所需的函数形式,然后将动作符号得到的值在赋给目标属性
\[<A> \rightarrow a_{\uparrow R}<B>_{\uparrow S}<C>_{\downarrow I}\\ i:=f(R,S)\]增加@f, 且$@f_{\downarrow I_1,I2 \uparrow S_1}, \ S_1 := f(I_1, I_2)$,于是找到合适的位置插入就好了。(不能破坏L-属性)
则通过枚举,容易得到以下改写后的SL-ATG
\[\begin{aligned} &\langle A\rangle \rightarrow a{ }_{\uparrow R} <B>_{\uparrow S} @ f_{\left\downarrow I_1, I_2 \uparrow S_1\right.}\langle C\rangle \\ &\mathrm{I}_1:=\mathrm{R}, \quad \mathrm{I}_2:=\mathrm{S}, \quad \mathrm{S}_1:=\mathrm{f}\left(\mathrm{I}_1, \mathrm{I}_2\right), \quad \mathrm{I}:=\mathrm{S}_1 \end{aligned}\]若为无参函数过程,其可以作为常数出现在简单复制形式的右部。
递归下降翻译
属性就是参数,继承属性就是为赋值形参,传值,综合属性就是返回值或者说变量形参,传地址,二者本质一样,将返回值赋值到地址上就等同于得到其返回值。